L’univers des cartes du monde
La carte du monde, le planisphère, ou encore la mappemonde, est un objet familier pour tous.
On se souvient sans doute des cartes de notre enfance en papier, pédagogiques et colorées, avec lesquelles nous découvrions la géographie, les pays et leurs capitales.
Aujourd’hui, la carte du monde conserve le même pouvoir et même plus, elle est universelle : nous orienter, décorer nos murs, rêver et voyager, évoquer des souvenirs, nourrir la curiosité et inspirer l’évasion.
Reconnaissable entre toutes par la silhouette de ses continents, elle parle à chacun, quel que soit son pays, son histoire ou ses rêves. Qui ne situe pas son pays, sa ville ou le trajet de ses anciens voyages devant un Planisphère? Qui ne rêve pas d’aller ici ou là lorsqu’on pose les yeux sur une Mappemonde?
Derrière cette image familière se cache un riche passé. Nous vous proposons de découvrir cette histoire, faite d’innovations, d’évolutions et de renaissances au fil des siècles.
La Mappemonde
Toutes les véritables Mappemondes que l’on possède actuellement représentent une vision du monde archaïque, avec des distances souvent fausses ou imprécises. Aujourd’hui, 1 100 mappa mundi nous viennent du Moyen-Âge.
La Rose de Vent
Les Roses de Vents au Moyen-Âge indiquaient l’est en haut afin de pouvoir placer Jérusalem, la ville sainte, à un niveau supérieur. Le nord en n’est devenu une norme qu’à partir du XVIIᵉ siècle!
Leur histoire
Un peu de vocabulaire
Le Globe Terrestre
L’un des premiers Globes connus apparait dans l’Antiquité vers 150 avant J.-C., illustrant les terres alors imaginées. Le plus ancien encore conservé date de 1492.
Aux XVIIᵉ et XVIIIᵉ siècles, les Globes deviennent des symboles de prestige, trônant dans les bibliothèques des érudits et des princes.
Le Planisphère
D’autant que notre planète n’est pas parfaitement sphérique, mais plutôt une ellipsoïde.
Par définition, un Planisphère est donc inexact, et chaque type de carte naît avec le souci de se rapprocher le plus fidèlement possible de la géographie complexe de notre planète.
La projection cartographique
Mais passons les mathématiques ! Penchons-nous plutôt sur les différentes projections cartographiques qui ont jalonnées l’histoire de la Carte du Monde.
Les projections, des plus classiques aux plus extravagantes
Les projections de Mercator, Gall Peters et Mollweide
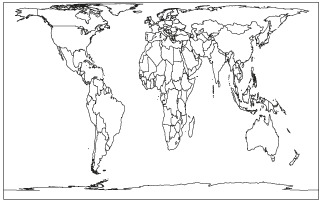
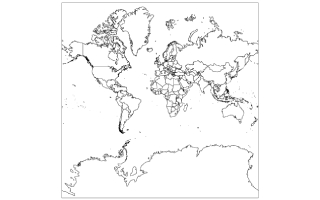
Il existe plusieurs variantes de la projection de Mercator, les différences se portent sur l’espacement des parallèles. En réalité, même si le nom de Mercator est couramment utilisé et est sans doute le nom de projection le plus connu, les Cartes du Monde les plus vues de nos jours correspondent plutôt à ses fameuses variantes : on peut citer la projection de Marin de Tyr, la projection de Gall, et la projection de Miller, par exemple. Elles possèdent la même caractéristique qui est de défomer les surperficies relatives, mais ont le mérite de de les minimiser.
C’est pour remédier à ses déformations que James Gall, suivi de Arno Peters, proposèrent leur propre projection qui conserve les superficies relatives : la projection de Gall-Peters. Il s’agit d’un compromis puisqu’à l’inverse, elle ne préserve pas les angles ce qui rend les continents difformes et par conséquent moins esthétiques.
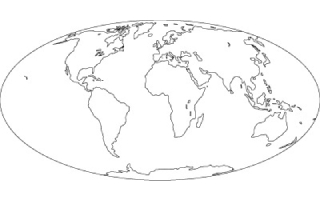
La projection de Mollweide aussi appelée projection de Babinet, quant à elle, est une autre façon de conserver les surfaces relatives, mais toujours au détriment des angles. Cette projection assez connue est fréquemment utilisée pour les planisphères en raison de son caractère compact.
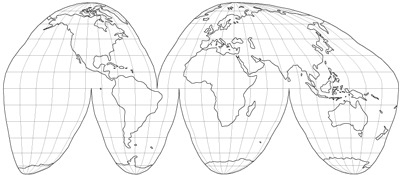
La projection de Goode
La projection de Postel

Emblème de l’ONU
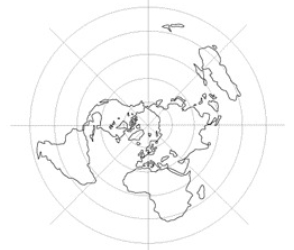
Projection de Postel
La projection de Cassini
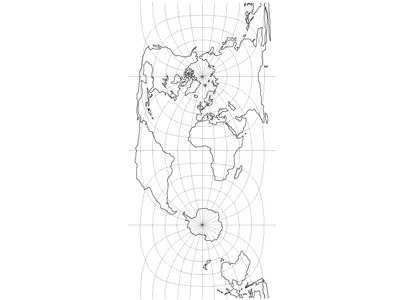
La projection d’Albers
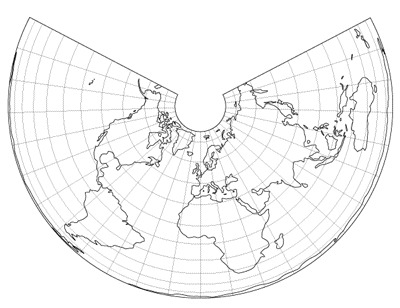
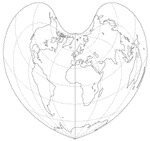
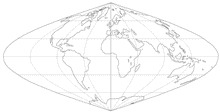
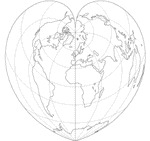
Les projections de Bonne, Sanson Flamsteed et Werner
- La projection de Sanson-Flamsteed: la parallèle d’origine est l’équateur.
- La projection de Werner: la parallèle d’origine est un pôle.
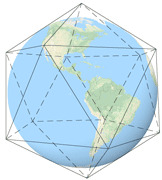
La projection de Fuller
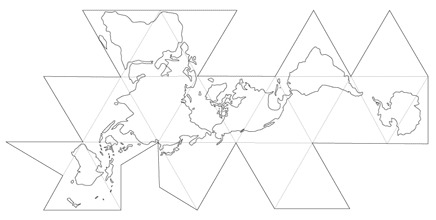
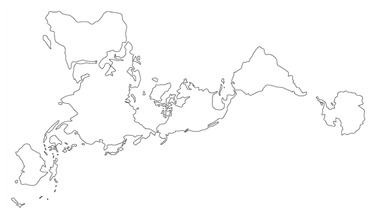
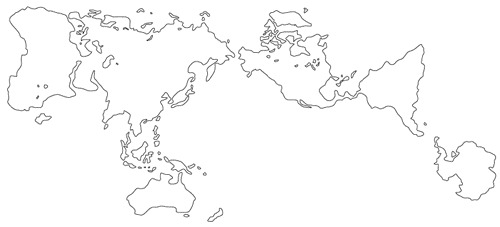
La projection Authagraph
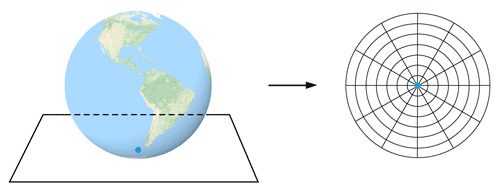
La classification des projections cartographiques
Mode de construction
Mode de construction
Résultat: Les méridiens sont des droites concourantes. Les parallèles sont des cercles concentriques, équidistants ou non.
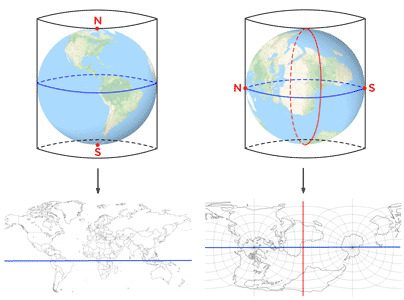
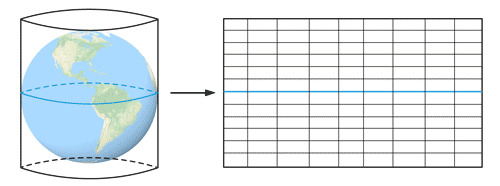
Les projections cylindriques
Résultat: Les méridiens et les parallèles sont de droites perpendiculaires entre elles. Les parallèles sont équidistantes ou non.
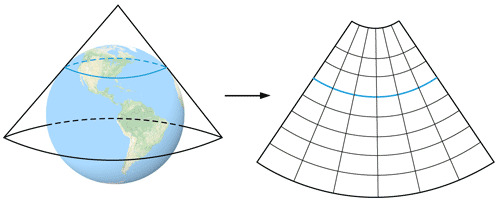
Les projections coniques
Résultat: Les méridiens sont des droites concourantes. Les parallèles sont des cercles concentriques, équidistants ou non.
Altérations géographiques
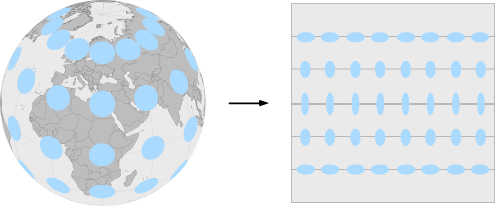
Les projections équivalentes
Résultat: La superficie des indicatrices de tissot n’est pas déformée, contrairement à leur forme.
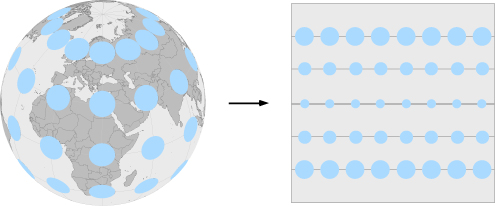
Les projections conformes
Résultat: La forme des indicatrices de Tissot n’est pas déformée, contrairement à leur superficie.
Les projections aphylactiques ou quelconques
Résultat: La forme et la superficie des indicatrices de Tissot sont déformées.
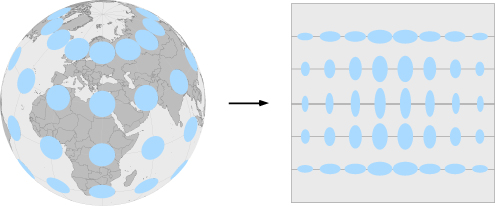
En résumé
Mercator
1569
1580
1745
1780
1805
1580
1745
1780
Livraison offerte
Expédié sous 4 à 8 jours ouvrés, avec date par e-mail, puis SMS pour gérer la livraison ou choisir un point relais.

Paiements sécurisés
En 1x ou 4x dès 30 €.
Données 100 % protégées.
Retours sous 14 jours
Pas satisfait(e) ?
Renvoyez votre commande.

Service client premium
clients@originalmap.fr (Lun–Ven, 9h–18h). Produit endommagé ? Une photo suffit pour un renvoi gratuit.
Original Map®, la référence en cartes décoratives et instructives
COLLECTIONS
Avec Reliefs
Effet Aquarelle
Classique
Satellite
Physique
Géo politique
Topographique 3D
Avec Antarctique
Avec Drapeaux
Centré Pacifique
Cartes France
Cartes Continents
Cartes Ciel
Haut de gamme
À personnaliser
Equal Earth
Gall-Peters
Stuart McArthur
Miller
Van der Grinten
Wagner
Winkel-Tripel
Nos Engagements
Savoir-Faire
Nos Clients
Inspiration
Voyager avec nos Cartes
BESOIN D'AIDE ?
Choix des Matières
Conseils d’Utilisation
Livraison & Retour
Mandat Administratif
Contact
Liste d’Envie
Bons de Réduction
Nos Cartes du Monde sont disponibles dans plusieurs langues et livrées dans le monde
Conditions Générales de Vente - Mentions légales - Politique de confidentialité - Gestion des cookies
